Results
For the problem described before I found 16146 solutions, and none of those solutions can be made from another one by flipping or rotating the board, so they are really different. Here (156 kByte) is the file containing all of them (zipped ASCII-text), one written in each row. You can view them using the applet on this page.On the input line below you can fill in all the numbers of a solution (for example 0 2 7 11 104 89 233 107 113 132 185 31 97). You can also choose not to display certain pentominos by simply not writing the corresponding number or by putting a '*' in its place (for example 0 2 7 11 104 89 * 107 * * * * *).
square positions?
There are solutions for every position of the square:| position | possible solutions |
|---|---|
| 0 | 5027 |
| 1 | 3207 |
| 2 | 987 |
| 3 | 1839 |
| 4 | 1662 |
| 5 | 582 |
| 6 | 1288 |
| 7 | 721 |
| 8 | 768 |
| 9 | 65 |
Pairs of blocks
There are some pairs of blocks which, if found in a solution, can easily be turned around in some way to get another solution. This list surely isn't complete!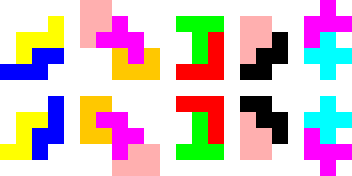
Some details derived from the solutions:
Thanks to php and mysql, evaluating the results has not been that hard...But be careful: the details presented below don't make much sense. I have only examined my set of non-symmetric solutions, and the results below vary with the precautions you choose not to find symmetric solutions. So it would be good to create the set of all possible solutions, including symmetric ones, and work on that. But to be honest: I'm too lazy. I wanted to create an algorithm which finds non-symmetric solutions quite fast and derive some things from them; this is done and I quit here.
I had a focus on the position of the square, so I started leaving out symmetric solutions by only allowing certain positions of the square (numbered 0 to 9, use the applet to view them). The calculation of the rest of them was avoided by only using certain positions of the long bar (five blocks in a row). I ended up with 269 distinct combinations of the long bar and the square which might lead to results and guaranteed that no symmetric solutions are found.
difficult and easy
A question which I found interesting: let's say n blocks are fixed on the board. Which ones do you have to use and where to put them so that they are the base for the highest/lowest number of solutions?n = 1
Difficult positions are easy to find and to list. The following table shows which block to put into which position so there is only one solution left for the whole board. You can use the column 'Solution' to view the board using the applet above (copy and paste works using linux/X11 ;-)
| BlockNr | Position | Solution |
|---|---|---|
| 2 | 83 | 1 0 * 251 98 41 320 8 10 132 251 7 97 |
| 2 | 135 | 9 0 * 227 5 59 163 77 127 5 94 3 17 |
| 2 | 165 | 0 2 * 170 96 138 286 45 39 117 122 13 52 |
| 2 | 198 | 1 47 * 0 98 18 321 33 13 39 212 2 130 |
| 2 | 210 | 7 48 * 4 1 107 299 57 96 130 132 25 132 |
| 3 | 13 | 0 28 116 * 135 65 2 83 33 124 228 11 87 |
| 3 | 199 | 6 39 136 * 97 94 157 76 29 101 202 18 48 |
| 5 | 51 | 0 28 16 244 134 * 142 107 68 72 255 31 91 |
| 5 | 112 | 0 31 191 45 178 * 5 137 68 108 218 28 59 |
| 6 | 13 | 0 3 100 244 250 47 * 138 104 82 230 25 24 |
| 6 | 137 | 0 28 251 221 134 107 * 2 96 72 81 25 14 |
| 6 | 213 | 8 32 234 1 78 107 * 77 126 29 22 3 129 |
| 6 | 295 | 1 39 237 0 251 40 * 138 9 115 97 27 120 |
| 12 | 39 | 9 0 237 112 59 102 254 41 91 32 251 9 * |
An easy solution for one fixed block is easily found and shown, too: take the square and put it into the corner to have 5027 possibilities left (0 * * * * * * * * * * * *).
n = 2
For n = 2, the solution is 0 2 * * * * * * * * * * *. So you have to put block 0 on position 0 and block 1 on position 2 to get the the highest number of solutions (1253) with two fixed blocks. The following table shows the highest numbers for every other combination of two blocks, too.
| - | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 |
| B0 | 1253 B0=0 B1=2 |
332 B0=0 B2=65 |
878 B0=1 B3=0 |
532 B0=1 B4=0 |
607 B0=0 B5=138 |
287 B0=3 B6=0 |
456 B0=0 B7=107 |
681 B0=3 B8=102 |
588 B0=0 B9=72 |
206 B0=0 B10=231 |
417 B0=0 B11=31 |
371 B0=0 B12=113 |
| B1 | - | 264 B1=0 B2=257 |
275 B1=0 B3=5 |
230 B1=3 B4=0 |
554 B1=0 B5=41 |
127 B1=0 B6=157 |
578 B1=0 B7=77 |
219 B1=0 B8=74 |
683 B1=2 B9=72 |
161 B1=3 B10=134 |
569 B1=0 B11=3 |
202 B1=2 B12=72 |
| B2 | - | - | 86 B2=4 B3=0 |
104 B2=65 B4=230 |
364 B2=230 B5=138 |
56 B2=4 B6=0 |
128 B2=257 B7=77 |
119 B2=230 B8=131 |
127 B2=230 B9=72 |
60 B2=230 B10=258 |
289 B2=257 B11=28 |
165 B2=65 B12=101 |
| B3 | - | - | - | 79 B3=0 B4=134 |
157 B3=0 B5=41 |
70 B3=38 B6=85 |
186 B3=97 B7=30 |
322 B3=1 B8=102 |
269 B3=191 B9=135 |
77 B3=258 B10=116 |
206 B3=97 B11=28 |
152 B3=251 B12=97 |
| B4 | - | - | - | - | 160 B4=0 B5=107 |
51 B4=38 B6=85 |
126 B4=251 B7=138 |
107 B4=0 B8=45 |
110 B4=191 B9=135 |
39 B4=0 B10=177 |
82 B4=0 B11=22 |
73 B4=200 B12=72 |
| B5 | - | - | - | - | - | 98 B5=138 B6=0 |
232 B5=138 B7=77 |
321 B5=138 B8=131 |
205 B5=138 B9=72 |
120 B5=138 B10=122 |
224 B5=138 B11=29 |
177 B5=138 B12=24 |
| B6 | - | - | - | - | - | - | 80 B6=157 B7=77 |
96 B6=157 B8=29 |
89 B6=240 B9=131 |
37 B6=0 B10=166 |
91 B6=0 B11=1 |
90 B6=233 B12=97 |
| B7 | - | - | - | - | - | - | - | 138 B7=138 B8=45 |
151 B7=143 B9=84 |
133 B7=107 B10=164 |
1064 B7=30 B11=28 |
125 B7=107 B12=132 |
| B8 | - | - | - | - | - | - | - | - | 141 B8=39 B9=36 |
78 B8=72 B10=2 |
138 B8=45 B11=22 |
103 B8=68 B12=113 |
| B9 | - | - | - | - | - | - | - | - | - | 60 B9=11 B10=231 |
173 B9=133 B11=28 |
247 B9=130 B12=132 |
| B10 | - | - | - | - | - | - | - | - | - | - | 93 B10=4 B11=7 |
51 B10=103 B12=36 |
| B11 | - | - | - | - | - | - | - | - | - | - | - | 133 B11=28 B12=100 |
n = 3
For n=3 it gets interesting...here are lots of tables showing the same for every combination of three blocks. The result is 0 2 * * * * * * * 72 * * * (504 solutions).
B0 and...
| - | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 |
| B1 | 126 B1=2 B2=230 B0=0 |
273 B1=0 B3=5 B0=3 |
201 B1=3 B4=0 B0=1 |
302 B1=0 B5=41 B0=1 |
79 B1=2 B6=199 B0=0 |
247 B1=24 B7=107 B0=0 |
219 B1=0 B8=74 B0=1 |
504 B1=2 B9=72 B0=0 |
132 B1=3 B10=134 B0=0 |
266 B1=24 B11=31 B0=0 |
144 B1=24 B12=113 B0=0 |
| B2 | - | 84 B2=4 B3=0 B0=1 |
83 B2=257 B4=178 B0=0 |
108 B2=230 B5=138 B0=6 |
38 B2=257 B6=0 B0=3 |
87 B2=230 B7=0 B0=6 |
112 B2=257 B8=102 B0=3 |
86 B2=120 B9=130 B0=1 |
33 B2=99 B10=198 B0=4 |
97 B2=257 B11=28 B0=0 |
60 B2=230 B12=96 B0=0 |
| B3 | - | - | 69 B3=0 B4=134 B0=1 |
143 B3=0 B5=41 B0=1 |
36 B3=0 B6=251 B0=1 |
106 B3=0 B7=138 B0=1 |
322 B3=1 B8=102 B0=3 |
142 B3=1 B9=0 B0=4 |
44 B3=258 B10=116 B0=1 |
124 B3=0 B11=2 B0=1 |
140 B3=0 B12=69 B0=1 |
| B4 | - | - | - | 150 B4=0 B5=107 B0=1 |
32 B4=100 B6=0 B0=3 |
48 B4=0 B7=143 B0=1 |
107 B4=0 B8=45 B0=1 |
91 B4=73 B9=72 B0=0 |
39 B4=0 B10=177 B0=1 |
67 B4=202 B11=7 B0=0 |
49 B4=0 B12=37 B0=1 |
| B5 | - | - | - | - | 74 B5=138 B6=0 B0=3 |
161 B5=138 B7=0 B0=6 |
139 B5=138 B8=23 B0=3 |
117 B5=138 B9=72 B0=0 |
53 B5=138 B10=122 B0=3 |
118 B5=138 B11=16 B0=0 |
132 B5=138 B12=24 B0=6 |
| B6 | - | - | - | - | - | 56 B6=219 B7=30 B0=0 |
44 B6=0 B8=23 B0=3 |
36 B6=292 B9=38 B0=0 |
20 B6=0 B10=166 B0=3 |
43 B6=0 B11=1 B0=4 |
52 B6=0 B12=1 B0=3 |
| B7 | - | - | - | - | - | - | 138 B7=138 B8=45 B0=1 |
71 B7=77 B9=36 B0=0 |
63 B7=107 B10=164 B0=4 |
335 B7=107 B11=31 B0=0 |
73 B7=107 B12=113 B0=0 |
| B8 | - | - | - | - | - | - | - | 141 B8=39 B9=36 B0=0 |
57 B8=45 B10=106 B0=1 |
138 B8=45 B11=22 B0=1 |
103 B8=68 B12=113 B0=0 |
| B9 | - | - | - | - | - | - | - | - | 60 B9=11 B10=231 B0=0 |
89 B9=36 B11=3 B0=0 |
126 B9=29 B12=119 B0=1 |
| B10 | - | - | - | - | - | - | - | - | - | 60 B10=4 B11=7 B0=0 |
49 B10=103 B12=36 B0=0 |
| B11 | - | - | - | - | - | - | - | - | - | - | 118 B11=5 B12=113 B0=0 |
B1 and...
| - | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 |
| B2 | 63 B2=230 B3=5 B1=0 |
51 B2=230 B4=59 B1=0 |
96 B2=230 B5=138 B1=2 |
40 B2=40 B6=233 B1=0 |
79 B2=230 B7=41 B1=0 |
56 B2=20 B8=110 B1=0 |
100 B2=230 B9=72 B1=2 |
36 B2=171 B10=201 B1=0 |
92 B2=257 B11=28 B1=27 |
65 B2=230 B12=96 B1=3 |
| B3 | - | 42 B3=99 B4=67 B1=3 |
125 B3=5 B5=138 B1=0 |
57 B3=38 B6=85 B1=0 |
89 B3=5 B7=41 B1=0 |
94 B3=1 B8=102 B1=55 |
144 B3=191 B9=135 B1=0 |
35 B3=45 B10=2 B1=0 |
66 B3=5 B11=3 B1=0 |
51 B3=139 B12=72 B1=2 |
| B4 | - | - | 64 B4=0 B5=107 B1=3 |
51 B4=38 B6=85 B1=0 |
53 B4=223 B7=107 B1=24 |
50 B4=135 B8=110 B1=0 |
105 B4=73 B9=72 B1=2 |
29 B4=202 B10=4 B1=2 |
67 B4=202 B11=7 B1=2 |
60 B4=200 B12=72 B1=0 |
| B5 | - | - | - | 38 B5=138 B6=164 B1=2 |
120 B5=132 B7=107 B1=24 |
119 B5=41 B8=10 B1=0 |
184 B5=138 B9=72 B1=2 |
36 B5=41 B10=213 B1=0 |
116 B5=132 B11=31 B1=24 |
76 B5=41 B12=9 B1=0 |
| B6 | - | - | - | - | 52 B6=85 B7=30 B1=0 |
85 B6=85 B8=110 B1=0 |
56 B6=85 B9=135 B1=0 |
24 B6=85 B10=119 B1=0 |
73 B6=85 B11=28 B1=0 |
52 B6=85 B12=54 B1=0 |
| B7 | - | - | - | - | - | 94 B7=41 B8=8 B1=0 |
64 B7=143 B9=72 B1=2 |
59 B7=77 B10=69 B1=0 |
484 B7=77 B11=3 B1=0 |
89 B7=77 B12=110 B1=0 |
| B8 | - | - | - | - | - | - | 97 B8=110 B9=135 B1=0 |
76 B8=72 B10=2 B1=0 |
109 B8=110 B11=28 B1=0 |
80 B8=110 B12=54 B1=0 |
| B9 | - | - | - | - | - | - | - | 51 B9=72 B10=141 B1=2 |
98 B9=72 B11=15 B1=2 |
146 B9=72 B12=50 B1=2 |
| B10 | - | - | - | - | - | - | - | - | 63 B10=4 B11=7 B1=2 |
33 B10=58 B12=130 B1=27 |
| B11 | - | - | - | - | - | - | - | - | - | 116 B11=3 B12=110 B1=0 |
B2 and...
| - | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 |
| B3 | 24 B3=5 B4=59 B2=230 |
39 B3=5 B5=138 B2=230 |
20 B3=191 B6=218 B2=257 |
51 B3=5 B7=41 B2=230 |
65 B3=1 B8=102 B2=257 |
50 B3=191 B9=135 B2=257 |
18 B3=15 B10=4 B2=135 |
38 B3=191 B11=28 B2=257 |
27 B3=99 B12=35 B2=257 |
| B4 | - | 35 B4=59 B5=138 B2=230 |
20 B4=38 B6=85 B2=20 |
59 B4=177 B7=143 B2=4 |
34 B4=8 B8=118 B2=4 |
38 B4=191 B9=135 B2=171 |
16 B4=202 B10=4 B2=197 |
49 B4=230 B11=28 B2=65 |
22 B4=178 B12=59 B2=257 |
| B5 | - | - | 19 B5=138 B6=164 B2=230 |
57 B5=138 B7=0 B2=230 |
119 B5=138 B8=131 B2=230 |
62 B5=138 B9=72 B2=230 |
29 B5=138 B10=258 B2=230 |
76 B5=138 B11=27 B2=230 |
59 B5=138 B12=96 B2=230 |
| B6 | - | - | - | 38 B6=85 B7=61 B2=257 |
36 B6=85 B8=110 B2=257 |
32 B6=157 B9=132 B2=40 |
12 B6=251 B10=105 B2=132 |
30 B6=85 B11=28 B2=257 |
32 B6=157 B12=57 B2=40 |
| B7 | - | - | - | - | 56 B7=61 B8=110 B2=257 |
51 B7=138 B9=101 B2=97 |
32 B7=143 B10=46 B2=4 |
92 B7=107 B11=31 B2=44 |
36 B7=61 B12=54 B2=257 |
| B8 | - | - | - | - | - | 36 B8=110 B9=135 B2=20 |
22 B8=50 B10=4 B2=197 |
44 B8=110 B11=28 B2=20 |
36 B8=110 B12=54 B2=257 |
| B9 | - | - | - | - | - | - | 19 B9=130 B10=215 B2=120 |
39 B9=135 B11=28 B2=257 |
57 B9=130 B12=132 B2=120 |
| B10 | - | - | - | - | - | - | - | 50 B10=116 B11=28 B2=257 |
26 B10=83 B12=97 B2=120 |
| B11 | - | - | - | - | - | - | - | - | 46 B11=28 B12=59 B2=257 |
B3 and...
| - | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 |
| B4 | 38 B4=0 B5=107 B3=119 |
36 B4=191 B6=85 B3=38 |
36 B4=78 B7=77 B3=1 |
36 B4=191 B8=110 B3=38 |
57 B4=134 B9=72 B3=0 |
23 B4=0 B10=177 B3=119 |
36 B4=78 B11=3 B3=1 |
24 B4=191 B12=54 B3=38 |
| B5 | - | 16 B5=107 B6=77 B3=119 |
52 B5=138 B7=41 B3=5 |
65 B5=138 B8=102 B3=1 |
62 B5=41 B9=130 B3=119 |
19 B5=138 B10=40 B3=5 |
39 B5=138 B11=29 B3=98 |
28 B5=138 B12=24 B3=98 |
| B6 | - | - | 28 B6=209 B7=143 B3=45 |
37 B6=85 B8=110 B3=38 |
40 B6=218 B9=135 B3=191 |
11 B6=0 B10=230 B3=97 |
31 B6=0 B11=1 B3=136 |
28 B6=85 B12=54 B3=38 |
| B7 | - | - | - | 87 B7=41 B8=102 B3=1 |
83 B7=30 B9=101 B3=97 |
43 B7=30 B10=230 B3=97 |
182 B7=30 B11=28 B3=97 |
44 B7=41 B12=69 B3=0 |
| B8 | - | - | - | - | 56 B8=110 B9=135 B3=191 |
35 B8=72 B10=2 B3=45 |
71 B8=102 B11=3 B3=1 |
48 B8=110 B12=54 B3=191 |
| B9 | - | - | - | - | - | 40 B9=131 B10=116 B3=258 |
96 B9=101 B11=28 B3=97 |
89 B9=130 B12=132 B3=119 |
| B10 | - | - | - | - | - | - | 44 B10=230 B11=28 B3=97 |
26 B10=103 B12=36 B3=112 |
| B11 | - | - | - | - | - | - | - | 55 B11=5 B12=36 B3=112 |
B4 and...
| - | B6 | B7 | B8 | B9 | B10 | B11 | B12 |
| B5 | 14 B5=0 B6=204 B4=198 |
69 B5=89 B7=107 B4=104 |
42 B5=138 B8=131 B4=19 |
46 B5=89 B9=38 B4=104 |
22 B5=107 B10=177 B4=0 |
61 B5=89 B11=31 B4=104 |
51 B5=41 B12=9 B4=101 |
| B6 | - | 31 B6=85 B7=30 B4=38 |
48 B6=85 B8=110 B4=38 |
28 B6=85 B9=135 B4=191 |
16 B6=218 B10=119 B4=135 |
43 B6=85 B11=28 B4=38 |
24 B6=85 B12=54 B4=191 |
| B7 | - | - | 33 B7=143 B8=9 B4=177 |
38 B7=143 B9=84 B4=200 |
20 B7=40 B10=190 B4=176 |
64 B7=77 B11=3 B4=78 |
39 B7=143 B12=72 B4=200 |
| B8 | - | - | - | 41 B8=110 B9=135 B4=191 |
26 B8=39 B10=140 B4=2 |
41 B8=110 B11=28 B4=135 |
32 B8=110 B12=54 B4=191 |
| B9 | - | - | - | - | 20 B9=39 B10=140 B4=2 |
50 B9=72 B11=15 B4=6 |
49 B9=84 B12=72 B4=200 |
| B10 | - | - | - | - | - | 27 B10=4 B11=7 B4=202 |
18 B10=102 B12=12 B4=0 |
| B11 | - | - | - | - | - | - | 37 B11=5 B12=36 B4=178 |
B5 and...
| - | B7 | B8 | B9 | B10 | B11 | B12 |
| B6 | 21 B6=47 B7=136 B5=107 |
44 B6=0 B8=23 B5=138 |
28 B6=240 B9=131 B5=107 |
18 B6=0 B10=178 B5=138 |
24 B6=74 B11=30 B5=107 |
26 B6=250 B12=36 B5=77 |
| B7 | - | 60 B7=77 B8=23 B5=138 |
53 B7=143 B9=68 B5=0 |
36 B7=30 B10=61 B5=107 |
142 B7=77 B11=3 B5=138 |
53 B7=0 B12=24 B5=138 |
| B8 | - | - | 62 B8=131 B9=72 B5=138 |
31 B8=72 B10=2 B5=83 |
57 B8=96 B11=25 B5=107 |
33 B8=131 B12=96 B5=138 |
| B9 | - | - | - | 24 B9=126 B10=122 B5=138 |
41 B9=0 B11=27 B5=37 |
69 B9=130 B12=132 B5=24 |
| B10 | - | - | - | - | 56 B10=122 B11=29 B5=138 |
45 B10=213 B12=9 B5=41 |
| B11 | - | - | - | - | - | 119 B11=29 B12=24 B5=138 |
B6 and...
| - | B8 | B9 | B10 | B11 | B12 |
| B7 | 48 B7=30 B8=110 B6=85 |
32 B7=30 B9=135 B6=85 |
18 B7=107 B10=12 B6=27 |
51 B7=30 B11=28 B6=181 |
26 B7=77 B12=1 B6=0 |
| B8 | - | 56 B8=110 B9=135 B6=85 |
24 B8=110 B10=119 B6=85 |
68 B8=110 B11=28 B6=85 |
48 B8=110 B12=54 B6=85 |
| B9 | - | - | 16 B9=135 B10=61 B6=85 |
40 B9=135 B11=28 B6=85 |
54 B9=132 B12=97 B6=233 |
| B10 | - | - | - | 24 B10=119 B11=28 B6=85 |
19 B10=178 B12=1 B6=0 |
| B11 | - | - | - | - | 32 B11=28 B12=54 B6=85 |
B7 and...
| - | B9 | B10 | B11 | B12 |
| B8 | 49 B8=110 B9=135 B7=30 |
39 B8=56 B10=164 B7=107 |
109 B8=45 B11=22 B7=138 |
36 B8=110 B12=54 B7=30 |
| B9 | - | 25 B9=133 B10=19 B7=30 |
139 B9=84 B11=27 B7=143 |
117 B9=84 B12=72 B7=143 |
| B10 | - | - | 84 B10=127 B11=25 B7=143 |
41 B10=103 B12=36 B7=77 |
| B11 | - | - | - | 111 B11=27 B12=72 B7=143 |
B8 and...
| - | B10 | B11 | B12 |
| B9 | 24 B9=133 B10=65 B8=110 |
61 B9=135 B11=28 B8=110 |
57 B9=72 B12=50 B8=8 |
| B10 | - | 43 B10=4 B11=7 B8=50 |
24 B10=65 B12=54 B8=110 |
| B11 | - | - | 48 B11=28 B12=54 B8=110 |
B9 and...
| - | B11 | B12 |
| B10 | 34 B10=256 B11=21 B9=101 |
25 B10=231 B12=8 B9=11 |
| B11 | - | 122 B11=27 B12=72 B9=84 |
B10 and...
| - | B12 |
| B11 | 34 B11=12 B12=113 B10=231 |